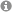Profile
Exploring Complex Quantum Systems
Research in our group comprises two major branches:
Quantum condensed matter theory, in particular the physics of topological insulators and two-dimensional conductors (read more).
Quantum chaos of many-body systems, bridging, via semiclassical path integral methods, classical chaos of interacting particles and quantum properties such as many-body interference and entanglement (read more).
For a complete overview of our research activities please have a look to the group’s publications.
Quantum condensed matter theory
In broad terms, our research focuses on electronic transport and time-dependent dynamics in mesoscopic systems, in particular topological insulators, graphene and further two-dimensional layers or hybrids of those. Such systems are often characterized by emergent pseudo-relativistic physics. Corresponding novel classes of materials have been identified, which might enable a paradigm shift for future electronics. Many of these materials have in common that their itinerant electrons exhibit (pseudo‑)relativistic behaviour: for instance, in graphene, electrons behave as massless Dirac particles, enabling studies of relativistic phenomena “in a pencil trace”. In topological insulators, the electron spin is locked to the electron momentum, since relativistic spin-orbit coupling is inherent in the relevant band structure. Moreover, spin-orbit coupling at surfaces and in nanostructures influences electrical transport and enables novel topological phenomena. This leads to a large variety of anomalous quasiparticle dynamics, e.g. Klein tunneling and spin/anomalous Hall effect(s).
Present research is mainly funded by DFG through the Collaborative Research Center CRC 1277.
Recent highlights of our efforts include:
________________________________________________________________________
2021
________________________________________________________________________
Generating high harmonics in topological insulators
In a collaboration of the experimental groups of Rupert Huber (UR) and Ulrich Höfer (University of Marburg) with the group of Ferdinand Evers (UR) and us on the theory side, a novel mechanism for generating high-order harmonics in the surface states of a topological insulator has been discovered. When quasi-relativistic electrons are accelerated through the Dirac point by an intense lightwave, they abruptly reverse their velocity allowing for purely non-integer high-harmonics.
This work is published in Nature (May 2021)
Press release here.
__________________________________________________________________________________
Very weak bonds to artificial atoms formed by quantum corrals
Employing numerical simulations we have accompanied and explained experiments of the Giessibl group (UR), who explored the bonding properties of the quantum corral (a circle of 48 iron atoms placed on a copper surface) as an artificial atom using an atomic force microscope (AFM). The confined electronic states can form a bond to the front atom of the AFM. The measured forces are about 1/1000 of typical forces in atomically resolved AFM. The confined electrons showed covalent attraction to metal tips and Pauli repulsion to CO-terminated tips.
This work is published in Science (May 2021)
Press release here.
The work is also feautured in ChemistryWorld.
________________________________________________________________________
2020
________________________________________________________________________
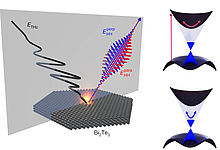
Probing Dirac Surface States via Quantum Capacitance
We model the electronic density of states probed by capacitance experiments of the Weiss group at UR in thin layers of the topological insulator BiSbTeSe2. The results point at the coexistence and intimate coupling of Dirac surface states with a bulk many-body phase (a Coulomb glass) in 3D-TIs.
This work is published in Nanoletters (November 2020)
__________________________________________________________________________________
Hexagonal Cyclotron Motion in Graphene Superlattices
In collaboration with the groups of R. Danneau (Karlsruhe) and M.-H- Liu (Tainan) we found that Dirac quasiparticles originating from graphene superlattice minibands do not undergo conventional cyclotron motion but follow more subtle trajectories. In particular, dynamics at low magnetic fields is characterized by peculiar, straight trajectory segments. Our results open up novel possibilities to use periodic potentials in electron optics experiments.
This work is published as an Editor’s suggestion in Physical Review Letters (November 2020)
Press release here.
__________________________________________________________________________________
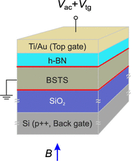
Novel Gate-Tunable Two-Dimensional Superlattices in Graphene
Together with our long-term collaborator, M.-H- Liu (Tainan), we provided theory support for experiments of the Eroms/Weiss group at UR, using a new technique for gate-tunable superlattices in graphene by the combined action of a back gate and a few-layer graphene patterned bottom gate. Thereby, well-pronounced satellite Dirac points and signatures of the Hofstadter butterfly are observed in corresponding transport measurements and theoretically explained.
This work is published in Nanoletters (October 2020)
__________________________________________________________________________________
Spin relaxation in superconductors: resonant vs. off-resonant spin-flip scatterering
In a joint work with D. Kochan and colleagues from the Fabian group at UR, we investigate the relaxation of quasiparticle spins in graphene proximitized by an s-wave superconductor in the presence of resonant magnetic and spin-orbit active impurities. We show that for resonant scattering the spin relaxation decreases with decreasing temperature, opposite to what is known for off-resonant scattering.
This work is published in Physical Review Letters (August 2020)
__________________________________________________________________________________
The electronic thickness of graphene
Graphene is often considered the thinnest existing material, but how thick are two atomically close graphene layers? Together with the Ensslin group (Zurich) doing transport measurements and with our theory colleagues, M.-H. Liu (Tainan) and M. Kurpas (Katowice), performing transport calculations, we investigate the electrostatics of two twisted graphene layers. We determine the finite dielectric thickness of each graphene layer to be ≈ 2.6 Å.
This work is published in Science Advances (March 2020)
__________________________________________________________________________________
Trapping Dirac Fermions in a Quantum Magnetic Bottle
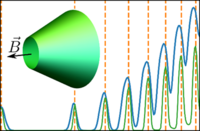We show that topological insulator nanocones exhibit intriguing mesoscopic surface transport phenomena, including the quantum Hall effect. Furthermore, a nanocone may act as a quantum magnetic bottle, confining surface Dirac electrons, leading to a largely interaction-dominated regime of Coulomb blockade type and, moreover, suggesting that TI nanocone junctions may serve as building blocks for Dirac electron optics setups.
This work is published as an Editor’s suggestion in Physical Review Letters (March 2020)
Press release here.
________________________________________________________________________
2018
________________________________________________________________________
Tuning Anti-Klein to Klein Tunneling in Bilayer Graphene
Together with experimental colleagues in Karlsruhe and M.-H. Liu (Tainan), we show that in gapped bilayer graphene, quasiparticle tunneling and the corresponding Berry phase can be controlled such that they exhibit features of single-layer graphene such as Klein tunneling.
________________________________________________________________________
2017
________________________________________________________________________
Dirac quantum time mirror
Both metaphysical and practical considerations related to time inversion have intrigued scientists for generations. Physicists have strived to devise and implement time-inversion protocols, in particular different forms of “time mirrors” for classical waves. Here we propose an instantaneous time mirror for quantum systems, i.e., a controlled time discontinuity generating wave function echoes with high fidelities. This concept exploits coherent particle-hole oscillations in a Dirac spectrum in order to achieve population reversal, and can be implemented in systems such as (real or artificial) graphene.
P. Reck, C. Gorini, A. Goussev, V. Krueckl, M. Fink and K. Richter
Physical Review B 95, 165421 (2017)
Article in InsideScience
__________________________________________________________________________________
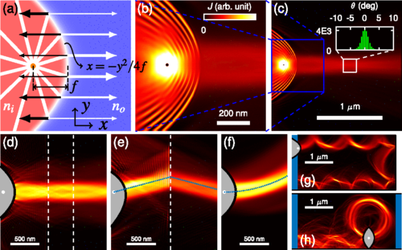
Creating and Steering Highly Directional Electron Beams in Graphene
We put forward a concept to create highly collimated, nondispersive electron beams in pseudorelativistic Dirac materials such as graphene or topological insulator surfaces. Combining negative refraction and Klein collimation at a parabolic pn junction, the proposed lens generates beams, as narrow as the focal length, that stay focused over scales of several microns and can be steered by a magnetic field without losing collimation.
M. Liu, C. Gorini and K. Richter
Physical Review Letters 118, 066801 (2017)
________________________________________________________________________
2015
________________________________________________________________________
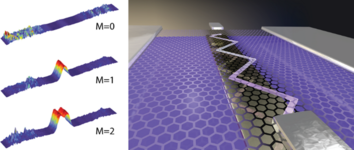
Guiding of Electrons in a Few-Mode Ballistic Graphene Channel
We provided theory support for experiments by the Schönenberger group on charge carriers guided in a suspended ballistic few-mode graphene channel, defined by electrostatic gating. By depleting the channel, a reduction of mode number and steps in the conductance were observed.
__________________________________________________________________________________
Scalable Tight-Binding Model for Graphene
Artificial graphene consisting of honeycomb lattices other than the atomic layer of carbon has been shown to exhibit electronic properties similar to real graphene. Here, we reverse the argument to show that transport properties of real graphene can be captured by simulations using “theoretical artificial graphene.” Our findings, together with M.-H. Liu, indicate that transport simulations for graphene can be efficiently performed with a strongly reduced number of atomic sites, allowing for reliable predictions for electric properties of complex graphene devices.
M. Liu, P. Rickhaus, P. Makk, E. Tóvári, R. Maurand, F. Tkatschenko, M. Weiss, C. Schönenberger and K. Richter
Physical Review Letters 114, 036601 (2015)
Quantum chaos of many-body systems
Having its roots in nuclear physics, the cross-disciplinary field of quantum chaos has swiftly developed since the 80ies, then with focus on the imprints of complex classical dynamics in corresponding quantum properties of single-particle systems. In recent years, the field has broadened towards many-body quantum chaos, vivid field in theoretical physics at the interface of statistical physics, nonlinear dynamics, many-body quantum dynamics in atomic and condensed matter and cosmology.
Many systems from all these distinctly different areas have in common that they reside at the semiclassical border between many-body classical chaos and quantum physics, in fact in a two-fold way: Far-out-of-equilibrium quantum dynamics involves high-energy excitations, associated with the usual short-wavelength limit, where wave mechanics approaches the limit of classical particles; alternatively, the thermodynamic limit of large particle numbers N can also be regarded as semiclassical, governed by an effective Planck constant 1/N.
Our research addresses fundamental questions that emerge at these complementary interfaces between the classical and quantum many-particle world. Thereby, lifting concepts from single-particle to many-body physics, semiclassical path integral techniques that are devised to bridge both realms, play a particular role in our research. The notion of “semiclassical” is meant here in the original sense of the limit of small Planck’s constant, hence clearly beyond classical physics.
Present research is mainly funded by DFG through the Reinhart Koselleck project "Many-Body Quantum Processes at the Edge of Chaos: From Non-Equilibrium Thermodynamics towards Quantum Gravity".
Recent highlights of our efforts include:
________________________________________________________________________
2023
__________________________________________________________________________________
Quantum survivors in a chaotic sea
Non-equilibrium quantum states formed from many particles are extremely fragile and usually do not survive for long, but "decay" rapidly: they thermalize due to chaos. In a recent publication we show that, intriguingly, there exist such survivors in ultracold atomic gases that, despite chaotic dynamics, perform hundreds of stable oscillations as a unique signature of stability and quantum coherence. The observation of such "many-body scars" opens up far-reaching implications for the occurrence and preparation of stable macroscopic quantum states.
__________________________________________________________________________________
Controlling Quantum Chaos: Optimal Coherent Targeting
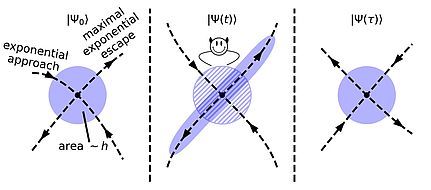
Chaotic dynamics has the propensity to be the villain of quantum device control as it leads rapidly to scrambling of quantum information and entropy production, certainly a fundamental hindrance to controlling quantum evolution. However, the question arises whether chaos, conversely, can be harnessed to control and efficiently guide the evolution of a complex quantum system toward desired, possibly unusual or particular states of matter, i.e. targeting. In effect, is it possible to mimic a quantum Maxwell demon to some extent. We recently showed how to extend targeting into the quantum realm in such an optimal coherent way.
The work has been published in Physical Review Letters.
________________________________________________________________________
2022
________________________________________________________________________
Semiclassical Roots of Universality in Many-Body Quantum Chaos (November 11, 2022)
Our Topical Review has been published in Journal of Physics A.
______________________________________________________________________________________
2021
________________________________________________________________________
A Renormalized Semiclassical Expansion in Quantum Critical Many-Body Systems
We have developed a general framework that shows how in the quasiclassical regime (N ≫ 1) the dynamics of an N-particle quantum system at a critical point is governed by an effective Planck constant, renormalized through the leading Lyaponov exponent. For scrambling in many-body hyperbolic systems, our results provide formal grounds to a conjectured multiexponential form of so-called out-of-time-ordered correlators.
This work is published in Physical Review Letters (March 2021)
________________________________________________________________________
2019
________________________________________________________________________
Far-out-of-equilibrium many-body quantum dynamics
Together with S. Tomsovic, P. Schlagheck and D. Ullmo we could semiclassically describe the far-out-of-equilibrium many-body quantum dynamics up to time scaled far beyond the Ehrenfest time.
__________________________________________________________________________________
Many-Body Quantum Interference in Chaotic Bosonic Systems
Quantum interference plays a prominent role in the far-out-of-equilibrium dynamics of many-body systems. Here, we examine a particular interference effect arising from discrete symmetries, which can significantly enhance quantum observables with respect to classical predictions. For the Bose-Hubbard model we further show strong evidence for the presence of dynamical localization.
This work is published in Physical Review Letters (November 2019).
__________________________________________________________________________________
Reversible quantum information spreading in many-body systems
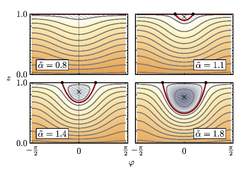Quantum chaotic interacting many-body systems are assumed to show fast and irreversible spreading of quantum information on short time scales. Here, we show that, in contrast to this common notion, certain quantum critical many-body systems exhibit oscillatory behavior between reentrant localization and delocalization of information in Hilbert space.
This work is published in Physical Review Letters (October 2019) __________________________________________________________________________________
Spectral Universality in Repulsive Bose Gases
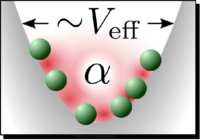We show that the crossover from an ideal Bose gas to the strongly correlated, fermionized gas exhibits universal behavior: Quantum systems from very few and up to many particles share the same underlying spectral features. Our method provides predictions for excitation spectra that enable access to finite-temperature thermodynamics in large parameter ranges.
This work is published in Physical Review Letters (June 2019)
________________________________________________________________________
2018
________________________________________________________________________
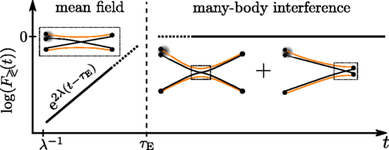
Many-Body Quantum Interference and the Saturation of Out-of-Time-Order Correlators
Our use of interfering paths in Fock space allowed us to provide a complete picture of both the exponential, short-time behavior and the saturation of so-called Out of Time Order Correlators in generic chaotic many body systems.
Josef Rammensee, Juan Diego Urbina, and Klaus Richter Phys. Rev. Lett. 121, 124101 (2018)
__________________________________________________________________________________
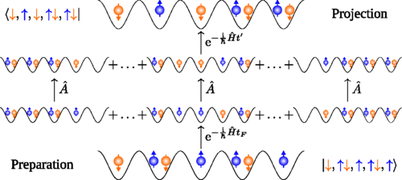
Many-body cousin of coherent backscattering
We predicted and further numerically confirmed the many-body analogue of coherent backscattering (and weak localization) due to interference between many-body paths in Fock space (together with P. Schlagheck)
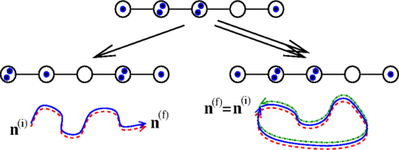
The many-body spin echo, now in the Fock space of Fermi-Hubbard systems, also belongs to this category.
Thomas Engl, Juan Diego Urbina, Klaus Richter, and Peter Schlagheck
Phys. Rev. A 98, 013630 (2018)
________________________________________________________________________
2016
________________________________________________________________________
Universal properties of Boson sampling
We addressed universal properties of the Boson sampling problem by means of many-body scattering in chaotic cavities using interfering paths.
________________________________________________________________________
2015
________________________________________________________________________
A Gutzwiller trace formula lifted to Many-Body Physics
The successful derivation of the many-body version of the celebrated Gutzwiler trace formula (in Fock space) that allows us to understand the spectra of Bose-Hubbard systems in terms of interfering periodic mean-field solutions is found here:
Thomas Engl, Juan Diego Urbina, and Klaus Richter
Phys. Rev. E 92, 062907 (2015)
Webredaktion - 28.06.2023 08:23 
