Research

      
Development of Green's function methods for electronic excitations & electron dynamics

GW is a Green's function methods and often regarded as state-of-the-art method to compute electronic band structures of solids. GW calculations are used to screen promising materials candidates for applications, or to calculate parameters for the use in models. Today's largest supercomputers are required when applying GW to systems with more than hundred atoms in the simulation. Such large-scale calculations are used to model nanoscale molecules and materials with interfaces and defects, for example tailor-made graphene structures used for all-carbon electronics [1,2] or complex two-dimensional materials [3].

We work on a low-scaling GW algorithm [1,3,4] to enable GW calculations on thousands of atoms. The computational cost of GW can be reduced to O(N²), where N is the number of atoms in the simulation. For two-dimensional materials, we have shown that low-scaling algorithms can reduce the computational cost by up to five orders of magnitude [3]. Our low-scaling GW algorithms are implemented in the widely used open-source package CP2K and have been highlighted in a community publication [5] and by the Gauss Center for Supercomputing. 

Our goal is to extend the low-scaling techniques to other electronic structure methods as the Bethe-Salpeter equation for excitons and to ultrafast electron dynamics.

We also apply our developed methods to pertinent problems in physics and chemistry, in close collaboration with experimental groups [2,6].

[1]  J. Wilhelm, D. Golze, L. Talirz, J. Hutter, C. A. Pignedoli: Toward GW calculations on thousands of atoms, J. Phys. Chem. Lett. 9, 306-312 (2018).

[2]  G. B. Barin, Q. Sun, J. Wilhelm, P. Ruffieux et al.: Growth optimization and device integration of narrow-bandgap graphene nanoribbons, Small 18, 2202301 (2022).

[3] M. Graml, K. Zollner, D. Hernangomez-Perez, P. E. Faria Junior, J. Wilhelm, Low-scaling GW algorithm applied to transition-metal dichalcogenide heterobilayers, J. Chem. Theory Comput. 20, 2202 (2024).

[4]  J. Wilhelm, P. Seewald, D. Golze: Low-scaling GW with benchmark accuracy and application to phosphorene nanosheets, J. Chem. Theory Comput. 17, 1662 (2021).

[5]  T. D. Kühne, M. Iannuzzi, J. Wilhelm, J. Hutter et al.: CP2K: An electronic structure and molecular dynamics software package - Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys. 152, 194103 (2020). 

[6] J. Am. Chem. Soc. 140, 3532-3536 (2018), J. Am. Chem. Soc. 141, 2843-2846 (2019), Nat. Commun. 10, 861 (2019), Nat. Chem. 14, 1061-1067 (2022)
    

      
Ultrafast electron dynamics

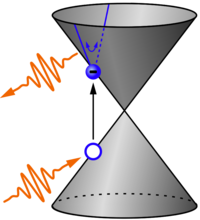Recent progress in laser technology made it possible to generate high-intensity ultra-short laser pulses. When irradiating materials with such a laser pulse, the electric field of the pulse accelerates electrons in the material, see sketch. Fingerprints of the ultrafast electron dynamics are encoded in the emission spectrum which is, however, often hard to interpret without a corresponding simulation. We simulate ultrafast electron dynamics to better understand the underlying mechanisms, for example of second-harmonic generation [7] (experiments conducted in the group of Giancarlo Soavi, Uni Jena), high harmonic generation [8,9] (experiments conducted in the group of Rupert Huber, UR) or direct-current generation [10]. For simulations, we employ our open-source package CUED [9].

Recently, we have developed analytical methods to calculate the response of materials to ultrashort laser pulses. This allows us to find analytical formulas for:

• the dc-like residual electric current that survives long after the laser illumination has died out [10]. Surprisingly this residual current can be almost as strong as the peak current under irradiation,
• the high-harmonic spectrum and how it depends on the carrier-envelope phase [11],
• the second-harmonic response of 2D materials [7] which enables the ultrafast readout of band occupations. This work has the potential for building ultrafast computers with Terahertz to Petahertz clock rate, orders of magnitude faster than the currently used technology with ~ 3 Gigahertz clock rate. 

Analytical calculations often come with approximations, like power series expansions We validate our analytical calculations with numerical simulations.

Our theoretical work also helps to interpret experiments conducted at the University of Regensburg, for example in the group of Rupert Huber [12]. 
    

[7] P. Herrmann, S. Klimmer, T. Lettau, T. Weickhardt, A. Papavasileiou, K. Mosina, Z. Sofer, I. Paradisanos, D. Kartashov, J. Wilhelm, G. Soavi, Nonlinear valley selection rules and all-optical probe of broken time-reversal symmetry in monolayer WSe2, accepted in Nat. Photonics (2024)

[8] C. P. Schmid, L. Weigl, P. Grössing, V. Junk, C. Gorini, S. Schlauderer, S. Ito, N. Hofmann, D. Afanasiev, J. Crewse, K. A. Kokh, O. E. Tereshchenko, J. Güdde, F. Evers, J. Wilhelm, K. Richter, U. Höfer, R. Huber, Tunable non-integer high-harmonic generation in a topological insulator, Nature 593, 385-390 (2021)

[9]  J. Wilhelm, P. Grössing, A. Seith, J. Crewse, M. Nitsch, L. Weigl, C. Schmid, F. Evers: Semiconductor Bloch-equations formalism: Derivation and application to high-harmonic generation from Dirac fermions, Phys. Rev. B 103, 125419 (2021).

[10] A. Seith, F. Evers, J. Wilhelm, Giant DC Residual Current Generated by Subcycle Laser Pulses, arxiv:2402.01490 (2024) (accepted in Phys. Rev. Res.)

[11] M. Graml, M. Nitsch, A. Seith, F. Evers, J. Wilhelm, Influence of chirp and carrier-envelope phase on noninteger high-harmonic generation, Phys. Rev. B 107, 054305 (2023).

[12] Nature 628, 329 (2024), Nat. Photonics 18, 595 (2024)